The phenomenon of breathing of electrical devices
There are a series of physical phenomena which concern all electrical devices in general, but which assume great importance in equipment for areas classified as hazardous for potentially explosive atmospheres. One of these phenomena is called "breathing".
by Andrea Battauz, R&D Manager of Cortem Group
Premise
There are a series of physical phenomena which concern all electrical devices in general, but which assume great importance in equipment for areas classified as hazardous for potentially explosive atmospheres.
One of these phenomena is called "breathing" by analogy to what happens in animals, in which the air from the external atmosphere enters the lungs through inspiration and expiration.
Unlike what happens in the animal world, where breathing is a primary activity indispensable for survival, in the case of electrical devices instead breathing is a secondary effect, unwanted, and usually having negative repercussions.
The phenomenon of breathing
In the figure we see the schematization of the breathing phenomenon in an electrical device. In it is represented a lamp with an incandescent bulb. Although this technology is now obsolete, it is very exemplary, because we have all had direct experience of the heat produced by these bulbs once they are turned on, burning ourselves when touched or perceiving the heat released even from a distance.
The reasoning made in this case can be made for any other electrical device, since each conductor in operation heats up due to the well-known Joule effect, which occurs in each conductor when the electric current passes due to the internal resistance other than zero.
In Figure 1, we can see the phenomenon of breathing, described in four phases:
1 – the device is off, and the internal atmosphere has the temperature T 1 and the pressure P 1 equal to those of the external atmosphere.
2 – the device is turned on, the air inside warms up and, passing to the temperature T 3 , dilates; the internal pressure would tend to increase, if the volume V 1 available to the internal atmosphere were sealed; in reality, the gaskets and typical seals which close an electrical device are unable to withstand even a small and short-term pressure difference; the internal air that expands comes out of the appliance, canceling the pressure differential between inside and outside, maintaining the initial pressure P 1 inside ; naturally, also the internal volume of the air, which is that of the electrical appliance, remains the same V 1.
3 – the device is now on and, after the initial transient, the temperature T 3 of the internal air (now higher than the external temperature) remains stable; since part of the air initially inside the device has gone out, its internal pressure remains equal to the external one and, therefore, equal to the initial pressure P 1 ; here too the internal volume of the air, which is always that of the lamp, is V 1 .
4 – the device is switched off and, in an inverse manner to phase 2, the air contained inside cools down and would tend to decrease its pressure but, since the device is not sealed, external air enters to rebalance the pressure which remains so still P 1 ; the internal volume of the air, which is always that of the lamp, is still V 1 .
In each on and off cycle, phases 1-4 are repeated, first causing the release of air from the electrical device and, subsequently, the suction of air from the external atmosphere, bringing a change of air inside the device in each cycle, indoor air with outdoor air.
In any case, this phenomenon would be negative as it is responsible for bringing pollutants and condensate inside the device, but it clearly becomes much more dangerous in a context such as that of potentially explosive atmospheres.
For this reason, even devices that use the Ex-e increased safety method of protection need to evaluate the internal temperatures, effectively considering the potentially dangerous internal air on a par with the external atmosphere.
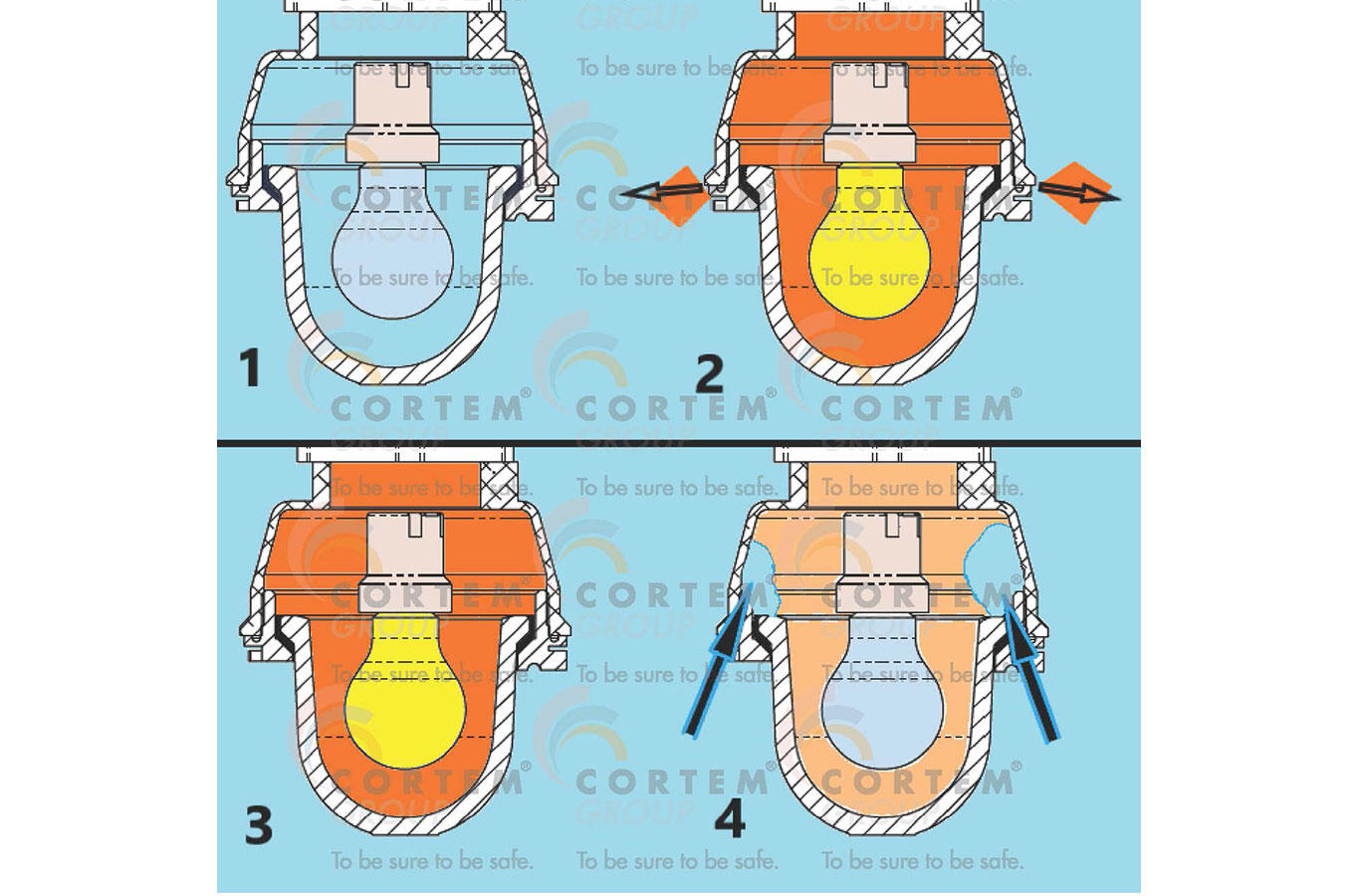
Fig. 1 The schematization of the breathing phenomenon in anelectrical device
The phenomenon of breathing with the gas law
The doubt may arise that the breathing phenomenon is imperceptible and insignificant or that many cycles (on/off) are required to bring a significant volume of external air inside a device.T
o try to make a quantification, suppose that air is an ideal gas and that it follows the equation of state of perfect gases: PV = n RT where P is the pressure of the gas inside the device, V its volume, n [1] its mass expressed in moles, R the ideal gas constant and T its temperature.
Let's try to calculate, in the light of this hypothesis, how much the moles (n) of gas contained within the volume of the lamp vary.
Initially we have (1) P 1 V 1 = n 1 RT 1 ;
when we turn on the lamp, the internal temperature increases up to an equilibrium situation T 3 of the internal air; in this passage part of the air initially inside the device has gone out passing from the initial mass n 1 (expressed in moles) n 3 while its internal pressure remains equal to the external one and, therefore, equal to the initial pressure P 1 ; here too the internal volume of the air, which is always that of the lamp, is V 1 ;
therefore we have (2) P 1 V 1 = n 3 RT 3 ;
now we turn off the lamp, in this inverse passage the conditions go back to being those of the lamp in phase 1 after a certain transient.
From the comparison (1) and (2) we have:
n 1 RT 1 = n 3 RT 3 then n 1 T 1 = n 3 T 3 and then n 3 = n 1 T 1 /T 3
n 3 is the mass of starting gas which remains in the hot device, while the mass of internal gas which is reciprocated in the cycle is Dn = n 1 - n 3 ; this naturally happens in every on/off cycle.
Evaluation of the phenomenon of breathing
Let's try to evaluate a practical case, the phenomenon of "breathing" produces in each cycle a turnover equal to
Dn = n 1 - n 3 = n 1 - n 1 T 1 /T 3 = n 1 (T 3 - T 1 ) / T 3
where T 1 and T 3 are expressed in degrees Kelvin.
Suppose that the gas in the lamp is initially at 20°C and it heats up by DT= 50°C we will have that:
T 1 =20°C= 293 K T 3 = 343 K >> Dn = n 1 (343 - 293) / 343 = 0.15 n 1 = 15% n 1
In this first cycle the turnover is 15% of the initial mass (85% remains in it) and so for each subsequent cycle the turnover is 15%. In the cycles following the first the starting mass is no longer the original one but has decreased by the "breathed" quantity, after the first cycle it corresponds to 85% of the original one, after the second cycle it is 85% of 85% of the original mass and so on.
Continuing the calculation, it is found that in about fifteen on/off cycles the replacement of the original mass with the environmental one is greater than 90%.
It can therefore be stated that, after around twenty cycles, the internal atmosphere is the same as that found outside and this must be considered when working in environments which may present potentially explosive atmospheres.
Conclusions
Anyone who designs devices suitable for use in areas classified as at risk of the formation of explosive atmospheres must know and take into due consideration the issue of breathing.
The various types of protection take this aspect into account and there is one, identified as "Ex- nR limited breathing devices ", which makes the limitation of this phenomenon its main prerogative.
To tell the truth, this type of protection is only suitable for Zone 2, as the level of protection it guarantees is not sufficient for use in Zone 1.
Notes and bibliographical references
[1] The mole is a unit of measurement for the mass or quantity of a substance; precisely a mole of a substance is the mass of that substance having a number of grams equal to its molecular weight; for example, one mole of H 2O, having molecular weight 1+1+16 = 18, corresponds to 18 grams of H2O; so 2 moles of H2O is 36 (=2*18) grams of H2O .